Generalized failure criterion proposed by Menétrey and Willam. More...

#include <MenetreyWillam.h>

Classes
struct	MenetreyWillamParameters

Public Types
enum	MenetreyWillamType { MenetreyWillamType::Mises, MenetreyWillamType::Rankine, MenetreyWillamType::DruckerPrager, MenetreyWillamType::MohrCoulomb }

Public Member Functions
	MenetreyWillam (const double ft, const MenetreyWillamType &type=MenetreyWillamType::Rankine, const double fc=0)

void	setParameters (const double ft, const double fc, const MenetreyWillamType &type)

template<typename T >
T	polarRadius (const double &theta) const

template<typename T >
std::pair< T, T >	dPolarRadius_dTheta (const T &theta) const

template<typename T >
T	yieldFunction (const ContinuumMechanics::HaighWestergaard::HaighWestergaardCoordinates< T > &hw, const double varEps=0.0) const

template<typename T >
std::tuple< T, T, T >	dYieldFunction_dHaighWestergaard (const ContinuumMechanics::HaighWestergaard::HaighWestergaardCoordinates< T > &hw, const double varEps=0.0) const

Static Public Member Functions
template<typename T >
static T	polarRadius (const T &theta, const double &e)

template<typename T >
static std::pair< T, T >	dPolarRadius_dTheta (const T &theta, const double &e)

template<typename T >
static std::tuple< T, T, T >	d2PolarRadius_dTheta2 (const T &theta, const double &e)

static double	abaqusMohrCoulombPotentialVarEpsToMenetreyWillam (const double varEps, const double psi)

static double	e (const double fc, const double ft)

static double	c (const double fc, const double ft)

static double	phi (const double fc, const double ft)

static double	ft (const double c, const double phi)

static double	fc (const double c, const double phi)

Public Attributes
struct Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::MenetreyWillamParameters	param

Detailed Description

Generalized failure criterion proposed by Menétrey and Willam.

Implementation of the generalized failure criterion proposed by Menétrey and Willam

\[ f(\xi,\rho,\theta) = \left(A_f\,\rho\right)^2+m\left(B_f\,\rho\,r(\theta,e)+C_f\,\xi\right) - 1 \]

with the Haigh-Westergaard coordinates $\xi,\,\rho,\,\theta$ and the parameters $A_f,\,B_f,\,C_f,\,m,\,e$ which are automatically evaluated dependent on the desired formulation (supported types see MenetreyWillamType).

Example

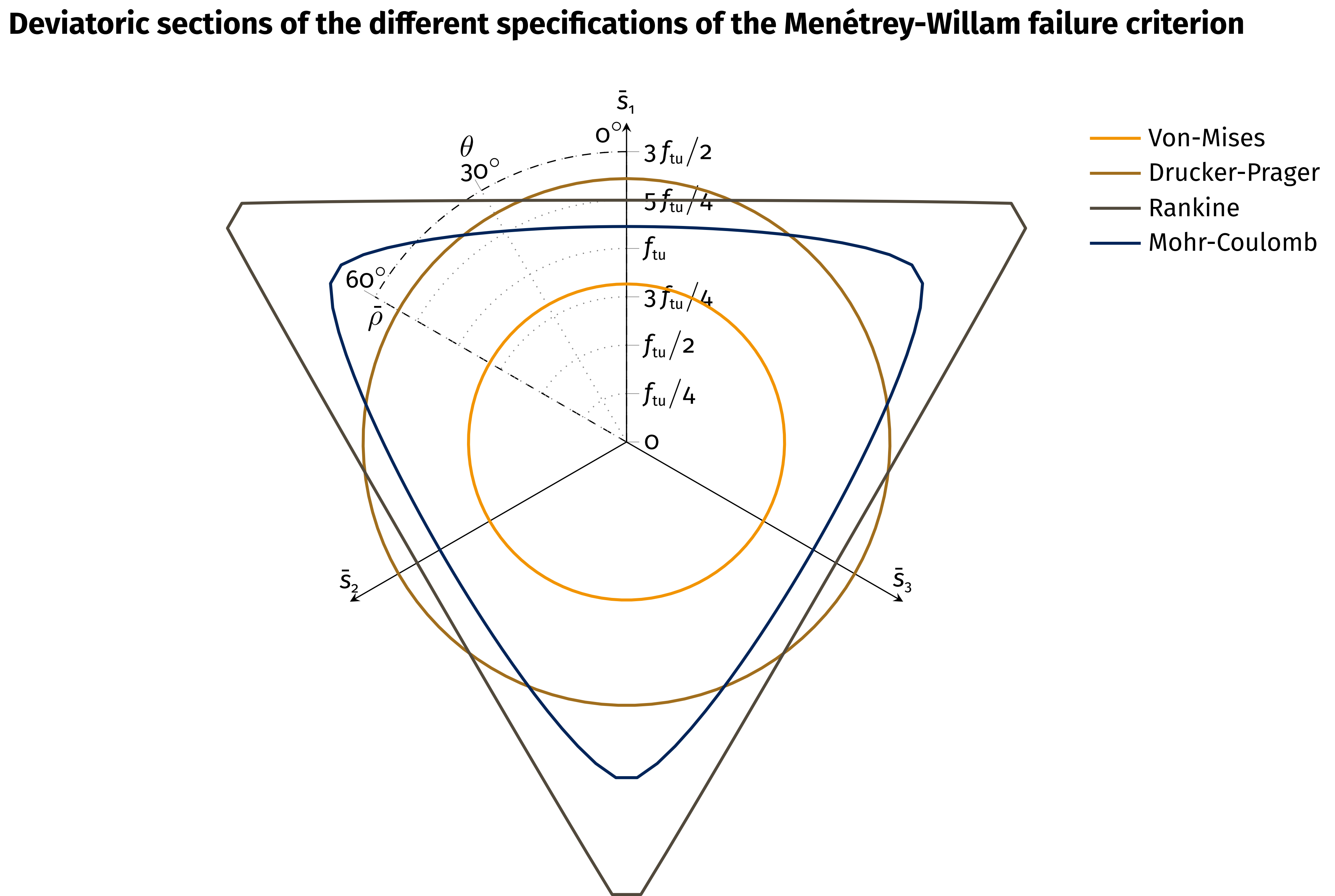
For a given pair of principal stress components in the Haigh-Westergaard stress space, evaluate the Mohr-Coulomb failure criterion:

#include <Marmot/MenetreyWillam.h>
#include <Marmot/HaighWestergaard.h>
 
using namespace Marmot;
 
void main()
{
  const double ft = 1.0;
  const double fc = 10.0;
  auto mw = MenetreyWillam( ft , MenetreyWillamType::MohrCoulomb, fc );
  const HaighWestergaard::HaighWestergaardCoordinates hw = { 1.0, -10, 0 };
  if ( mw.yieldCriterion( hw ) >= 0 ) 
    std::cout << "Material is yielding!" << std::endl;
  else
    std::cout << "Material is elastic!" << std::endl;
}

Class Documentation

◆ Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::MenetreyWillamParameters

struct Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::MenetreyWillamParameters

Aggregate of the parameters for the generalized strength criterion proposed by Menétrey and Willam.

Class Members
double	Af	additional parameter to capture the influence of the deviatoric stress invariant $\rho$
double	Bf	addditional parameter to capture the influence of the deviatoric stress invariant $\rho$ and the lode angle
double	Cf	addditional parameter to capture the influence of the hydrostatic stress invariant $\xi$
double	m	Friction parameter $m$
double	e	Eccentricity parameter $e$; to obtain a smooth and convex surface $e$ has to be in the range of $0.5\leq e \leq 1$

Member Enumeration Documentation

◆ MenetreyWillamType

enum Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::MenetreyWillamType

strong

Enumerator
Mises	von-Mises failure criterion; only the tensile strength ft has to be specified.
Rankine	Rankine failure criterion; only the tensile strength ft has to be specified. Note In deviatoric sections, compared to the original Rankine criterion the vertices are slightly rounded (specified by the eccentricity parameter $e$).
DruckerPrager	Drucker-Prager failure criterion; both the tensile strength ft as well as the compressive strength fc have to be specified.
MohrCoulomb	Drucker-Prager failure criterion; both the tensile strength ft as well as the compressive strength fc have to be specified. Note In deviatoric sections, compared to the original Mohr-Coulomb criterion the vertices are slightly rounded (specified by the eccentricity parameter $e$).

Constructor & Destructor Documentation

◆ MenetreyWillam()

Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::MenetreyWillam	(	const double	ft,
		const MenetreyWillamType &	type = `MenetreyWillamType::Rankine`,
		const double	fc = `0`
	)

Constructor that takes the uniaxial tensile strength $f_t$ and two optional arguments consisting of the specific type of failure criterion MenetreyWillamType and the uniaxial compressive strength $f_c$. The call of the constructor automatically fills the corresponding Menetrey-Willam param.

Member Function Documentation

◆ setParameters()

void Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::setParameters	(	const double	ft,
		const double	fc,
		const MenetreyWillamType &	type
	)

This function can be used to reset the type of the specified failure criterion by entering the uniaxial compressive strength fc, the uniaxial tensile strength ft and the MenetreyWillamType.

◆ polarRadius() [1/2]

template<typename T >

T Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::polarRadius ( const double & theta ) const

inline

Compute the polar radius $r$ from the Lode angle $\theta$. The eccentricity parameter will be used from the chosen Menetrey-Willam parameters param.

◆ polarRadius() [2/2]

template<typename T >

static T Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::polarRadius	(	const T &	theta,
		const double &	e
	)

inlinestatic

Static version for computing the polar radius $r$ from the Lode angle $\theta$ and a specified value for the eccentricity parameter $e$.

◆ dPolarRadius_dTheta() [1/2]

template<typename T >

std::pair< T, T > Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::dPolarRadius_dTheta ( const T & theta ) const

inline

Compute the polar radius $r$ and its derivative $\frac{dr}{d\theta}$ from the Lode angle $\theta$. The eccentricity parameter will be used from the param struct.

◆ dPolarRadius_dTheta() [2/2]

template<typename T >

static std::pair< T, T > Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::dPolarRadius_dTheta	(	const T &	theta,
		const double &	e
	)

inlinestatic

Static version for computing the polar radius $r$$ and its derivative $\frac{dr}{d\theta}$ from the Lode angle $\theta$ and a specified value for the eccentricity parameter $e$.

◆ d2PolarRadius_dTheta2()

template<typename T >

static std::tuple< T, T, T > Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::d2PolarRadius_dTheta2	(	const T &	theta,
		const double &	e
	)

inlinestatic

◆ yieldFunction()

template<typename T >

T Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::yieldFunction	(	const ContinuumMechanics::HaighWestergaard::HaighWestergaardCoordinates< T > &	hw,
		const double	varEps = `0.0`
	)		const

inline

Evaluate the yield function $f$ depending on the Haigh-Westergaard stress coordinates hw. $f<0$ means no yielding while $f\geq0$ means yielding. When the optional fillet parameter varEps is given, a potential vertex along the hydrostatic axis is rounded and thus a smooth failure criterion is obtained.

Note: The yield function can be also used as plastic potential function if needed.

◆ dYieldFunction_dHaighWestergaard()

template<typename T >

std::tuple< T, T, T > Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::dYieldFunction_dHaighWestergaard	(	const ContinuumMechanics::HaighWestergaard::HaighWestergaardCoordinates< T > &	hw,
		const double	varEps = `0.0`
	)		const

inline

Evaluate the derivatives of the yield function with respect to the Haigh-Westergaard stress coordinates, i.e. $df/d\xi,\,df/d\rho,\,df/d\theta$. When the optional fillet parameter varEps is given, a potential vertex along the hydrostatic axis is rounded. Thus, a smooth failure criterion is obtained, where derivatives can be calculated uniquely.

◆ abaqusMohrCoulombPotentialVarEpsToMenetreyWillam()

static double Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::abaqusMohrCoulombPotentialVarEpsToMenetreyWillam	(	const double	varEps,
		const double	psi
	)

inlinestatic

Compute a fillet parameter for the vertex of the yield surface along the hydrostatic axis in the same way as Abaqus does. This parameter is only relevant in the case of the Drucker-Prager or the Mohr-Coulomb criterion. The calculated smoothing value can then be used as the optional input argument varEps in yieldFunction and dYieldFunction_dHaighWestergaard.

◆ e()

static double Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::e	(	const double	fc,
		const double	ft
	)

inlinestatic

Compute the eccentricity parameter based on a given compressive strength fc and tensile strength ft.

◆ c()

static double Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::c	(	const double	fc,
		const double	ft
	)

inlinestatic

Compute the cohesion based on a given compressive strength fc and tensile strength ft.

◆ phi()

static double Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::phi	(	const double	fc,
		const double	ft
	)

inlinestatic

Compute the friction angle in radian based on a given compressive strength fc and tensile strength ft.

◆ ft()

static double Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::ft	(	const double	c,
		const double	phi
	)

inlinestatic

Compute the tensile strength based on a given cohesion c and a friction angle phi.

◆ fc()

static double Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::fc	(	const double	c,
		const double	phi
	)

inlinestatic

Compute the compressive strength based on a given cohesion c and a friction angle phi.

Member Data Documentation

◆ param

struct Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::MenetreyWillamParameters Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::param

The documentation for this class was generated from the following files:

modules/core/MarmotMechanicsCore/include/Marmot/MenetreyWillam.h
modules/core/MarmotMechanicsCore/src/MenetreyWillam.cpp

Classes

Public Types

Public Member Functions

Static Public Member Functions

Public Attributes

Detailed Description

Example

Class Documentation

◆ Marmot::ContinuumMechanics::CommonConstitutiveModels::MenetreyWillam::MenetreyWillamParameters

Member Enumeration Documentation

◆ MenetreyWillamType

Constructor & Destructor Documentation

◆ MenetreyWillam()

Member Function Documentation

◆ setParameters()

◆ polarRadius() [1/2]

◆ polarRadius() [2/2]

◆ dPolarRadius_dTheta() [1/2]

◆ dPolarRadius_dTheta() [2/2]

◆ d2PolarRadius_dTheta2()

◆ yieldFunction()

◆ dYieldFunction_dHaighWestergaard()

◆ abaqusMohrCoulombPotentialVarEpsToMenetreyWillam()

◆ e()

◆ c()

◆ phi()

◆ ft()

◆ fc()

Member Data Documentation

◆ param